Day 25: MoE 實作 (中) Auxiliary-Loss

2025 iThome 鐵人賽

DAY 25

AI & Data

實戰派 AI 工程師帶你 0->1系列第 25 篇

17th鐵人賽

jeremylee

2025-09-19 09:20:33

33 瀏覽

分享至

第二十五天: MoE 實作 Auxiliary-Loss

前情提要

昨天基本上已經把 inference 的 MoE 完成了，但還沒有談到如何平衡負載

參考文章 & 圖片來源:
https://www.cnblogs.com/rossiXYZ/p/18835426
https://arxiv.org/pdf/2408.15664

今天主要介紹兩個，一個是常見的平衡負載的aux loss function，另外是 loss-free 應用 DeepSeekV3。

面對負載不平衡，一種是透過 loss function 一種是不透過 loss function。

Aux Loss: 透過額外的 loss 來引導 gate 給出平衡的打分。
Auxiliary-Loss-Free Load Balancing: 不改變 gate 現有的打分結果，而是改變選取 top_k 這個分配方式。

1. 負載平衡

在前幾天基礎觀念的時候有提到，透過 Gating + top_k 可以選取特定的專家，但卻無法保證負載平衡，那為什麼負載平衡這麼重要呢? 那我們先想想為什麼會發生負載不平衡，以及會導致什麼情況。
通常是隨機初始化模型參數，所以在第一次 epoch 可能只有選到幾個專家(像昨天實作一樣)，那模型更新門控權重時，這些專家的權重被強化，這樣會導致少數專家過載，每次都需要處理大量的 token，然而其他專家沒訓練到，會導致效能下降(因為大模型通常會將 MoE 的 FFN 放在不同的 GPU 上，所以就變成那張 GPU 效能很低)，更不符合當初 MoE 的核心觀念"術業有專攻"。
所以為了改善上面的問題，就常見也是最先提出來的，就是添加輔助損失函數(Auxiliary-Loss)，那後來也有提出不透過損失函數的方式。

2. Auxiliary-Loss

先來看一下經典的兩篇 GShard, Switch Transformers，兩者提出的 loss function 蠻接近的，其中 fi 跟 Pi 的理想都是 1/N，假設有四個專家，那當然分配給每個專家全部的四分之一。

等下實作我們採用下圖。

圖片來源: https://arxiv.org/pdf/2408.15664

流程如下(程式參考 minimind):

Pi 其實就是 scores 的平均
使用 one_hot 來記錄每個 token 的 top_k 選擇，哪個專家被選到，就會在對應欄位為 1 → mask_ce
mask_ce 取平均 → ce
ce * expert 的數量 → fi
(ce 簡寫是沿用 GShard 的名詞)
fi * Pi 取總和再乘 alpha

從昨天的 MoEGate 多加一部份計算 loss 而已

import torch
from torch import nn
import torch.nn.functional as F

class MoEGate(nn.Module):
    def __init__(
            self,
            top_k, 
            hidden_size,
            n_routed_experts,
            alpha = 0.001
        ):
        super().__init__()
        
        self.top_k = top_k
        self.alpha = alpha
        self.n_routed_experts = n_routed_experts
        self.gate = nn.Linear(hidden_size, n_routed_experts, bias = False)

    def forward(self, x: torch.Tensor):
        '''
            x: (B, L, D)
        '''

        B, L, D = x.shape

        # step 1: 攤平 -> (B * L, D)
        x_flat = x.view(-1, D)

        # step 2: 透過 linear 計算 logits -> (B * L, n_routed_experts)
        logits = self.gate(x_flat)

        # step 3: 利用 softmax 計算 scores
        scores = F.softmax(logits, dim = -1)

        # step 4: 選取 top_k
        topk_scores, topk_idx = torch.topk(scores, k = self.top_k, dim = -1)

        # step 5: Normalize, 讓總和為 1
        topk_scores = topk_scores / (topk_scores.sum(dim = -1, keepdim = True) + 1e-6)

        aux_loss = 0
        if True: # self.training
            # Pi: gating 分數在 batch 維度上的平均
            Pi = scores.mean(0) # (n_routed_experts, )

            # 紀錄每個 token 的 top_k 選擇，哪個專家被選到，就會在對應欄位為 1 
            # 維度為 (B * L * top_k, n_routed_experts)
            mask_ce = F.one_hot(topk_idx.view(-1), num_classes = self.n_routed_experts)
            print(f'mask_ce: {mask_ce[:5]}')

            # 每個專家被選到的比例，總和為 1
            ce = mask_ce.float().mean(0) 
            print(f'ce: {ce}')

            # 乘上專家數量，把比例換算成專家負載比
            # 如果是平均分配 ce 會是 [1/N, 1/N, ...]
            # 那麼 fi 會是 [1, 1, ...]
            # 如果某個專家被特別多 token 選中，那它的 fi 就會大於 1。
            fi = ce * self.n_routed_experts 
            print(f'fi: {fi}')

            aux_loss = (fi * Pi).sum() * self.alpha 
            print(f'aux_loss: {aux_loss}')

        return topk_scores, topk_idx, aux_loss
    
if __name__ == "__main__":
    import random
    seed = 42
    random.seed(seed)
    torch.manual_seed(seed)
    x = torch.rand(2, 20, 8)
    gate = MoEGate(2, 8, 4)
    gate(x)

3. Auxiliary-Loss-Free

論文連結: https://arxiv.org/pdf/2408.15664
接著來看由上面論文提出，不使用 loss function，而是透過單一的 bias 改變選取 top_k 的方式，這麼做的好處，可以不影響模型原先的損失函數以及梯度計算。

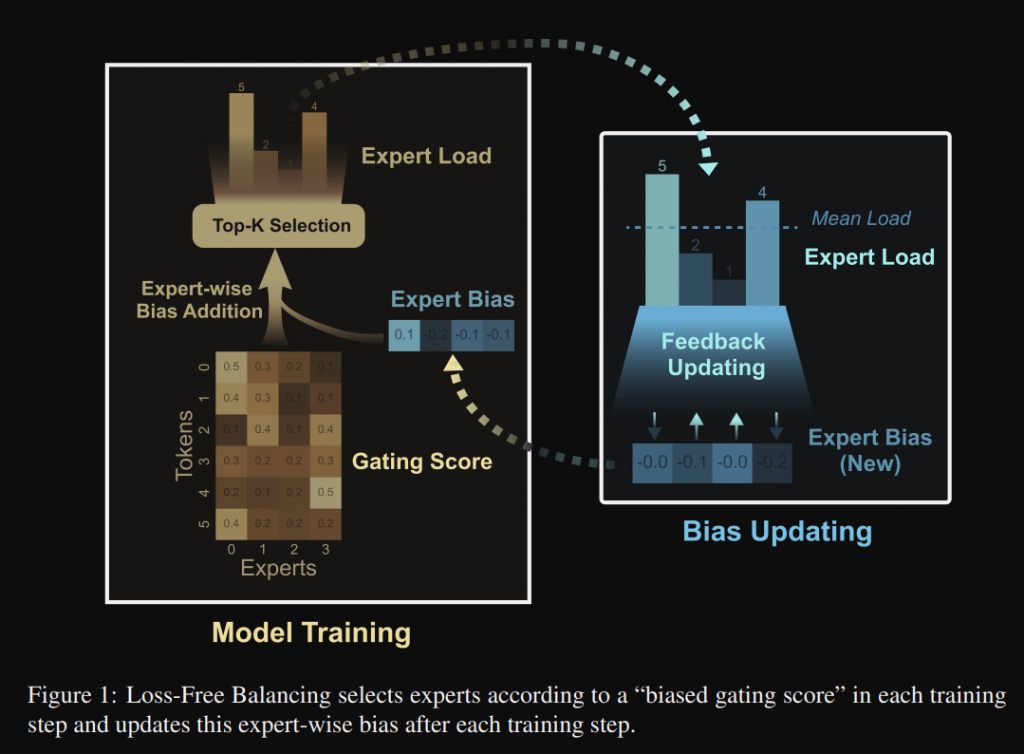
那數學式及流程圖如下，主要是藉由加入 bias 這項，來影響 top_k 的選擇。

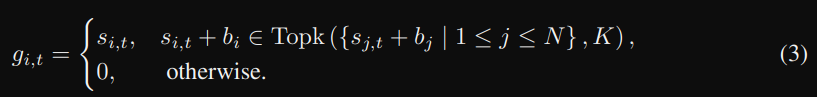
從上圖可以看到，如果專家 i 負載過高，則減少 bi，降低其被選中的機率。
那論文當中比較給出比較圖(如下)， loss-free 效果更好，而且簡潔有效。

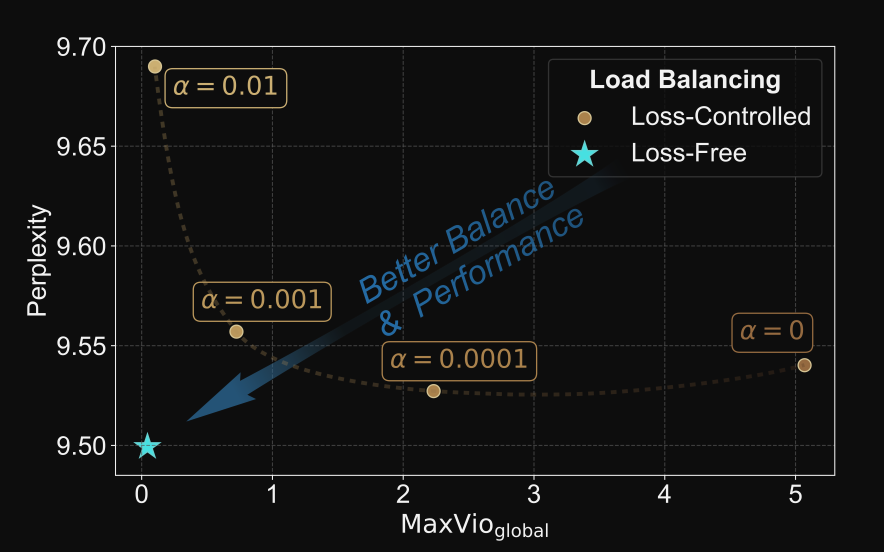
我們照著論文當中的步驟實作就行了
程式參考:
https://github.com/wajihullahbaig/deepseekv3-minimal/blob/main/models/deepseek_v3.py
https://blog.csdn.net/shizheng_Li/article/details/147685729

初始化 bi → nn.Parameter
在計算 top_k 之前，將 gating scores 和 bi 相加
(1) 剛跟剛才一樣使用 one hot ，紀錄每個 token 的 top_k 選擇，哪個專家被選到
(2) 總和得到 c_i, 再平均得到 c_i_bar
e_i = c_i_bar - c_i
將要更新的權重 torch.sign(e_i) 對 self.bias.data 加回去

import torch
from torch import nn
import torch.nn.functional as F

class MoEGateLossFree(nn.Module):
    def __init__(
            self,
            top_k, 
            hidden_size,
            n_routed_experts,
            alpha = 0.001
        ):
        super().__init__()
        
        self.top_k = top_k
        self.alpha = alpha
        self.n_routed_experts = n_routed_experts
        self.gate = nn.Linear(hidden_size, n_routed_experts, bias = False)

        self.bias = nn.Parameter(torch.zeros(n_routed_experts), requires_grad = False)

    def forward(self, x: torch.Tensor):
        '''
            x: (B, L, D)
        '''

        B, L, D = x.shape

        # step 1: 攤平 -> (B * L, D)
        x_flat = x.view(-1, D)

        # step 2.1: 透過 linear 計算 logits -> (B * L, n_routed_experts)
        logits = self.gate(x_flat)

        # step 3.1: 利用 softmax 計算 scores
        scores = F.softmax(logits, dim = -1)

        # step 3.2: 在計算 top_k 之前，將 gating scores 和 bi 相加
        scores = scores + self.bias

        # step 4: 選取 top_k
        topk_scores, topk_idx = torch.topk(scores, k = self.top_k, dim = -1)

        # step 5: Normalize, 讓總和為 1
        topk_scores = topk_scores / (topk_scores.sum(dim = -1, keepdim = True) + 1e-6)


        if True: # self.training
            # ~~~ 更新 bias (from Algorithm 1) ~~~
            # 跟剛才一樣用 one_hot，紀錄每個 token 的 top_k 選擇，哪個專家被選到
            # step 3 from Algorithm 1
            mask = F.one_hot(topk_idx, self.n_routed_experts).sum(dim = 1).float()
            expert_load = mask.sum(dim = 0) # c_i, 剛才 ce 是比例, 現在 c_i 是實際 token 數量
            avg_expert_load = expert_load.sum() / self.n_routed_experts # c_i_bar

            # step 4 from Algorithm 1
            load_violation_error = avg_expert_load - expert_load # e_i

            # step 5 from Algorithm 1
            with torch.no_grad():
                bias_updates = self.alpha * torch.sign(load_violation_error)
                self.bias.data += bias_updates
                
        return topk_scores, topk_idx

if __name__ == "__main__":
    import random
    seed = 42
    random.seed(seed)
    torch.manual_seed(seed)
    x = torch.rand(2, 20, 8)
    gate = MoEGateLossFree(2, 8, 4)
    gate(x)

今天的公式有些不是那麼直觀，而且更深度討論會有可不可以微分之類的，但這邊就沒有特別提到，只給出對應的程式，今天就先到這裡囉 ~~